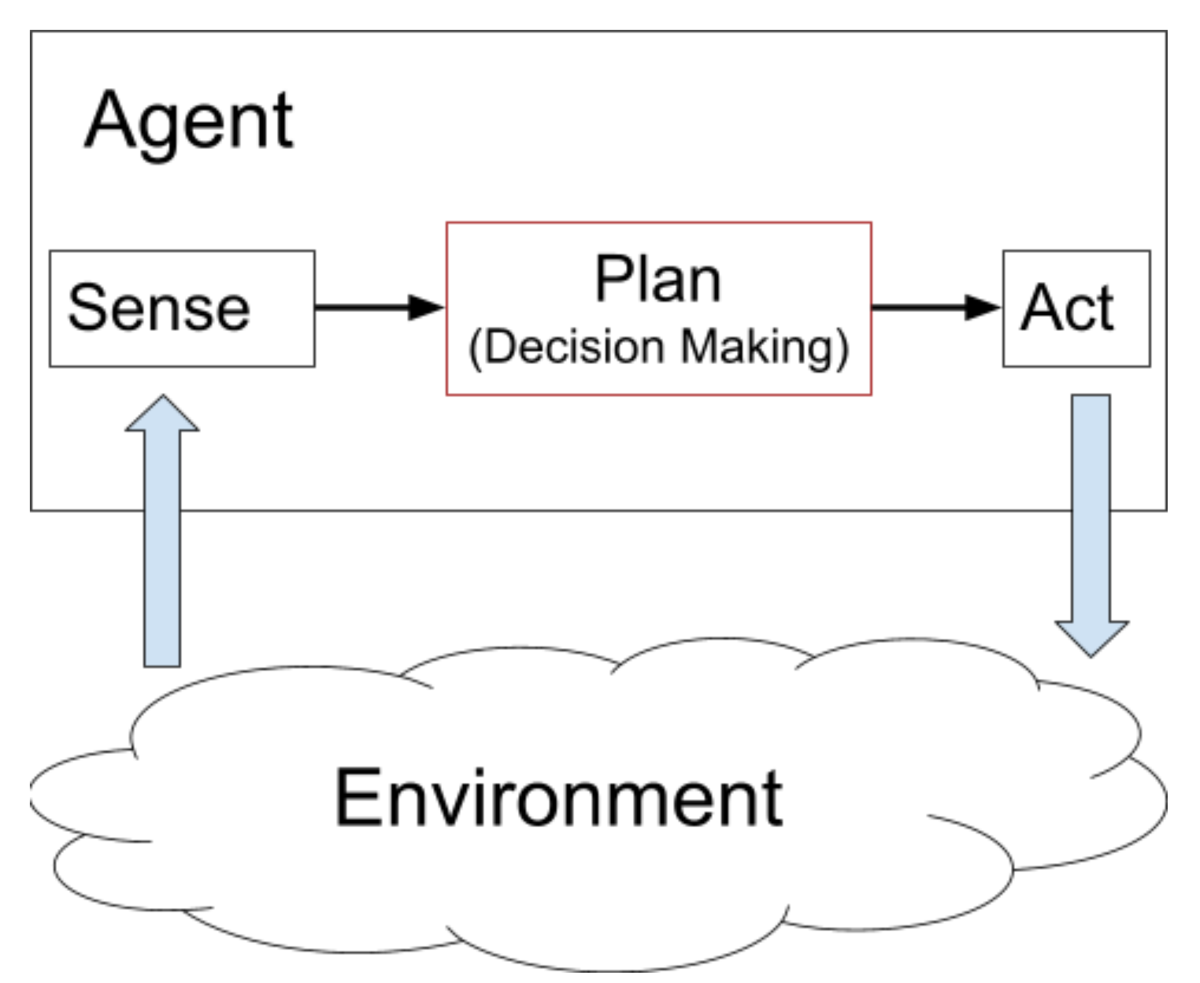
Autonomously controlling a car is challenging and requires solving a number of subproblems. If perception, which understands information from sensors, corresponds to the eyes or our system while control, which turns the wheel and adjusts the velocity, corresponds to the body having a physical impact on the car, then decision making is the brain. It must connect what is perceived with how the car is controlled.
In this blog post, we discuss the challenges in designing the brain of an autonomous car that can drive safely in a variety of situations. First, we introduce the scope and motivation for decision making before presenting how it is currently implemented in Autoware. We then talk about the trends observed in recent autonomous driving conferences and briefly introduce a few works that propose interesting new directions of research.
By the way, at Tier Ⅳ, we are looking for various engineers and researchers to ensure the safety and security of autonomous driving and to realise sharing technology for safe intelligent vehicles. Anyone who is interested in joining us, please contact us from the web page below.
Introduction to Decision Making
We spend our life making decisions, carefully weighing the pros and cons of multiple options before choosing the one we deem best. Some decisions are easy to make, while others can involve more parameters than can be considered by a single human. Many works in artificial intelligence are concerned with such difficult problems. From deciding the best path in a graph, like the famous Dijkstra or A* algorithms, to finding the best sequence of actions for an autonomous robot.
For autonomous vehicles, decision making usually deals with high level decisions and can also be called behavior planning, high-level planning, or tactical decision making. These high level decisions will then be used by a motion planner to create the trajectory to be executed by the controller. Other approaches consider planning as a whole, directly outputting the trajectory to execute. Finally, end-to-end approaches attempt to perform all functions in a single module by using machine learning techniques trained directly on sensor inputs. While planning is one of the functions handled by end-to-end techniques, we will not discuss them in this blog post as they tend to make decision making indistinguishable from perception and control.
The common challenge unique to decision making systems comes from the open-endedness of the problem, even for humans. For perception, a human can easily identify the different objects in an image. For control, a human can follow a trajectory without too many issues. But for decision making, two drivers might make very different decisions in the same situation and it is almost never clear what is the best decision at any given time. The goals of an autonomous car at least seem clear: reach the destination, avoid collisions, respect the regulations, and offer a comfortable ride. The challenge then comes from finding decisions that best comply with these goals. The famous “freezing robot problem” illustrates this well: once a situation becomes too complex, not doing anything becomes the only safe decision to make and the robot “freezes”. Similarly, the best way for a car to avoid collisions is not to drive. A decision system must thus often deal with conflicting goals. Challenges also arise from uncertainties in the perception and in the other agents. Sensors are not perfect and perception systems can make mistakes, which needs to be carefully taken into account as making decisions based on wrong information can have catastrophic consequences. Moreover, cars or pedestrians around the autonomous vehicle can act in unpredictable ways, adding to the uncertainty. Dedicated prediction modules are sometimes used and focus on generating predictions for other agents. The final challenge we want to mention here comes from dealing with occluded space. It is common while driving not to be able to perfectly perceive the space around the car, especially in urban areas. We might be navigating small streets with sharp corners or obstacles might be blocking the view (parked trucks for example), potentially hiding an incoming vehicle.
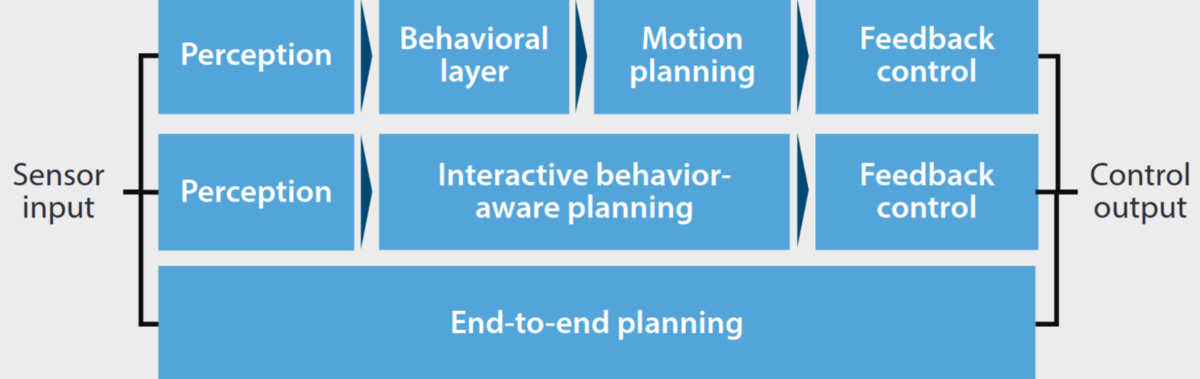
Figure 2 - Standard autonomous driving architecture
Schwarting, Wilko, Javier Alonso-Mora, and Daniela Rus. "Planning and decision-making for autonomous vehicles." Annual Review of Control, Robotics, and Autonomous Systems (2018)
To summarize, we are concerned with the problem of making decisions on the actions of the car based on perceptions from sensors and the main challenging points are:
- conflicting goals that require trade-offs;
- uncertainties from perception, localization, and from the other agents;
- occluded parts of the environment.
In the rest of this post we will try to introduce methods to make decisions and to tackle the aforementioned challenges.
Decision Making in Autoware
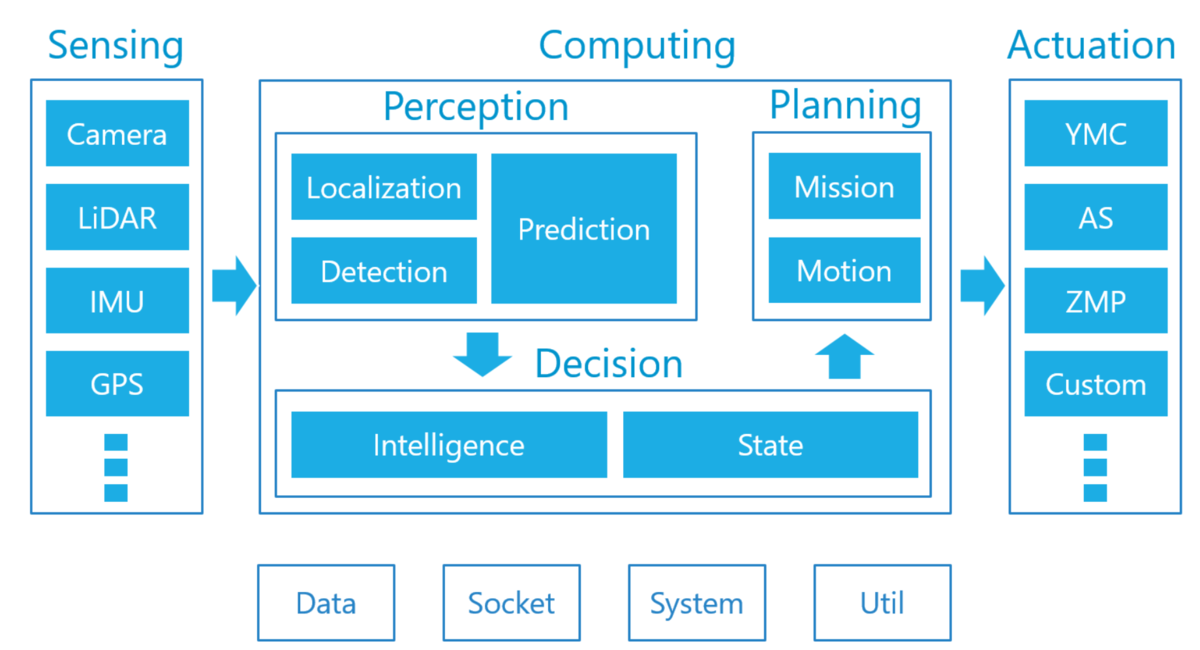
Autoware is an open source project providing a full stack software platform for autonomous driving including modules for perception, control and decision making. In the spirit of open source, its architecture is made to have each function be an independent module, making it easy to add, remove, or modify functionalities based on everyone’s own needs.
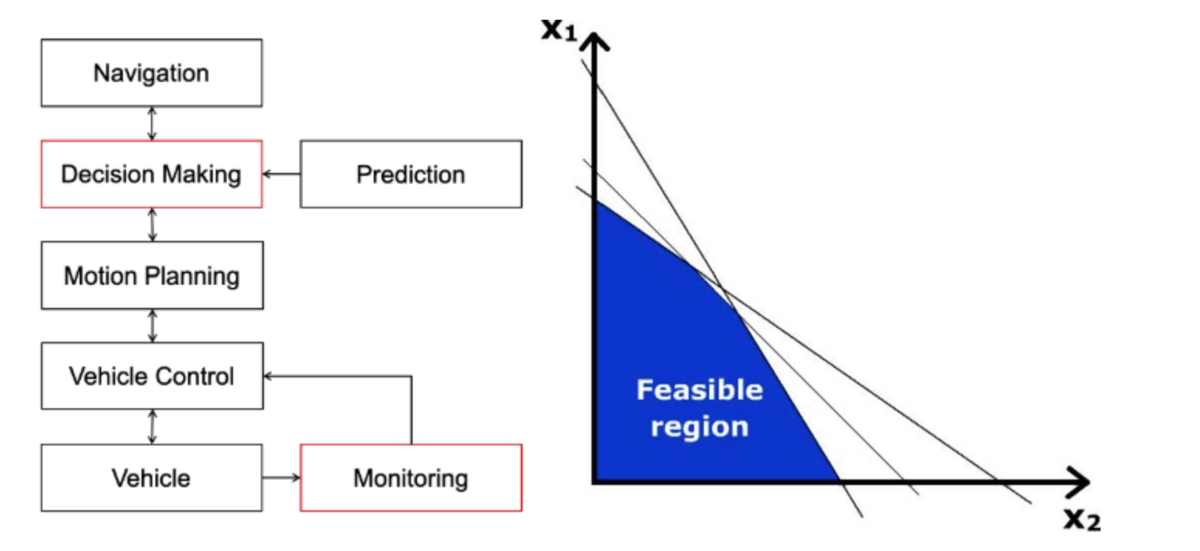
In this architecture, decision making occurs at two stages. At the Planning stage, various planning algorithms such as A* or the Model Predictive Control are used to plan and modify trajectories. Before that, at the Decision stage, the output of perception modules is used to select which planning algorithms to use for the current situation. For example, it can be decided that the car should perform a parking maneuver, in which case a specific parking module will be used (Motion Planning Under Various Constraints - Autonomous Parking Case - Tier IV Tech Blog). This Decision stage is implemented using a Finite State Machine (FSM), a common model used in rule-based systems. A state machine is basically a graph representing possible states of the system as nodes and the conditions to transition between these states as edges. State machines are easily designed by humans and offer decisions that are easy to understand and explain, which is very desirable in autonomous driving systems.
While the decision and planning modules of Autoware offer state-of-the-art driving in nominal cases, they are not well suited to deal with uncertainties or occluded space. There are no classical approaches to deal with these challenges but they are studied by a lot of ongoing research, which we will discuss in the next part.
Current Trends
We now introduce some of the most popular approaches for decision making seen in recent autonomous driving conferences (the IEEE Intelligent Vehicles Symposium and the International Conference on Intelligent Transportation Systems).
Deep Reinforcement Learning (DRL) is an application of deep neural networks to the Reinforcement Learning framework where the goal is to learn what action works best at each state of the system, corresponding to a policy Π(s) = a representing the decision a to take at state s. This usually requires learning a function Q(s,a) which estimates the reward we can obtain when performing action a at state s. In simple environments, this function can be computed by completely exploring the search space but when the state and action spaces become too large, like in autonomous driving problems, more advanced techniques must be used. DRL leverages the power of deep neural networks to approximate the function Q(s,a), allowing the use of RL in very complex situations. This requires training on a large number of example situations, which are usually obtained using a simulator. The biggest issue with using these techniques on real vehicles is the difficulty to guarantee the safety of the resulting policy Π(s). With large state spaces, it is difficult to ensure that there does not exist a state where the policy will take an unsafe action.
Mixed-Integer Programming (MIP) is an optimization technique which maximizes a linear function of variables that are under some constraints. Some of these variables must be restricted to integer values (e.g., 0 or 1) and can be used to represent decisions (e.g., whether a lane change is performed or not). The problem of an autonomous vehicle following a route can be represented with MIP by including considerations like collisions and rules of the road as constraints. Using commonly available solvers, the problem can then be solved for an optimal solution, corresponding to the best values to assign to the variables while satisfying the constraints. Many approaches applying MIP to autonomous driving have been proposed and while they can solve many complex situations, they cannot handle uncertain or partial information and require accurate models of the agents and of the environment, making them difficult to apply to real-life situations.
Monte-Carlo Tree Search (MCTS) is an algorithm from game-theory which is used to model multiplayer games. It is most famous for being used in AlphaGo, the first program able to defeat a human professional at the game of Go. The MCTS algorithm assumes a turn-based game where agents act in succession and builds a tree where each node is a state and where a child is the expected result from an action. If complete, the tree represents the whole space of possible future states of the game. Because building a complete tree is impossible for most real problems, algorithms use trial-and-error, similar to reinforcement learning, to perform sequences of actions before simulating the resulting outcome. This approach has the advantage of considering the actions of other agents in relation to our own decisions, making it useful in collaborative scenarios where the autonomous vehicle must negotiate with other vehicles (e.g., in highway merges). The main issue with MCTS is their computational complexity. As the tree must be sufficiently explored in order to confidently choose actions, it can be hard to use in real-time situations.
In the next section, we will present some recent works related to each of these trends.
Interesting Works
Graph Neural Networks and Reinforcement Learning for Behavior Generation in Semantic Environments
Patrick Hart(1) and Alois Knoll(2)
1- fortiss GmbH, An-Institut Technische Universität München, Munich, Germany.
2- Chair of Robotics, Artificial Intelligence and Real-time Systems, Technische Universität München, Munich, Germany.
IEEE Intelligent Vehicles Symposium (2020) https://arxiv.org/abs/2006.12576
An issue with reinforcement learning is that their input is usually a vector of fixed size. This causes issues when tackling situations with varying numbers of other agents. This paper proposes to use Graphic Neural Networks (GNNs) to learn the policy of a reinforcement learning problem. GNNs are a neural network architecture that uses graphs as inputs instead of vectors, offering a solution that is more flexible and more general than previous works.
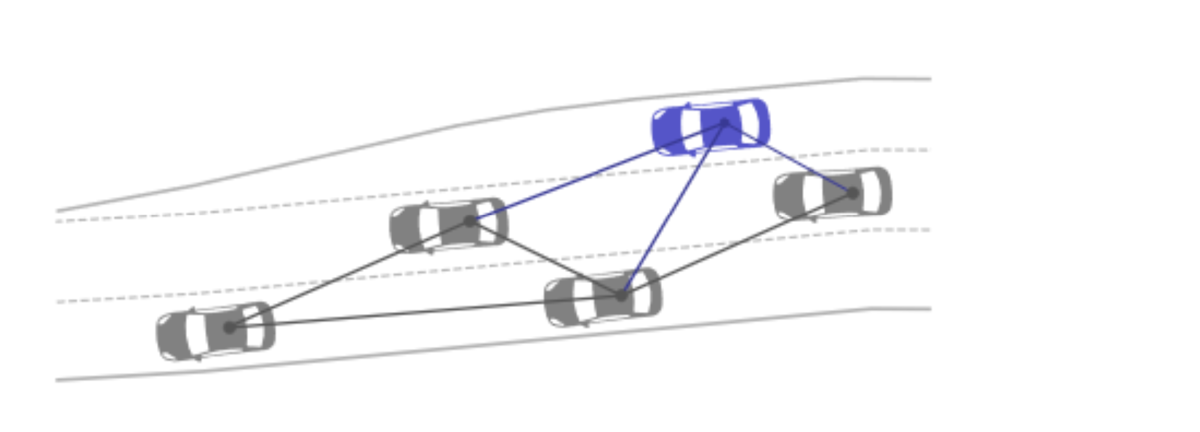
The graph used in this paper represents vehicles with the nodes containing state information (coordinates and velocities) and the edges containing the distance between two vehicles. Experiments on a highway lane change scenario are used to compare the use of GNNs against the use of traditional neural networks. It shows that while results are similar in situations close to the ones used at training time, the use of GNNs generalizes much better to variations in the input without a significant loss of performance.
Autonomous Vehicle Decision-Making and Monitoring based on Signal Temporal Logic and Mixed-Integer Programming
Yunus Emre Sahin, Rien Quirynen, and Stefano Di Cairano
MITSUBISHI ELECTRIC RESEARCH LABORATORIES
American Control Conference (2020) https://www.merl.com/publications/TR2020-095
This work uses Mixed-Integer Programming to represent the problem of finding intermediate waypoints along a given route. The interesting parts of this work are its use of Signal Temporal Logic (STL) to represent some of the constraints, and a monitoring system that can identify if the environment changes in ways that deviate from the models used.
Temporal Logic is a language used to write rules which include some time information. In this work for example, intersections are regulated by a first-in-first-out rule, which in STL is written as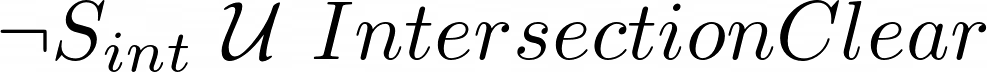 
, which means “the car must not be at the intersection until it is clear”. The paper proposes an efficient way to encode STL rules as constraints, reducing the solution space of the problem (like in Figure 5b) and ensuring that they are satisfied by the solution of the MIP.
The paper tackles a simulated scenario with intersections and curved roads and shows that their solution can navigate a number of situations in real-time. They also show that their monitoring system can correctly detect unexpected changes in the environment, for example when another vehicle suddenly brakes. It is then possible to fall back to another algorithm or to solve the MIP problem again but with the new information added. This alleviates the main issue of MIP which is to depend on very good models of the environment as it is now possible to detect when these models make a mistake.
Accelerating Cooperative Planning for Automated Vehicles with Learned Heuristics and Monte Carlo Tree Search
Karl Kurzer(1), Marcus Fechner(1), and J. Marius Zöllner(1,2)
1- Karlsruhe Institute of Technology, Karlsruhe, Germany
2- FZI Research Center for Information Technology, Karlsruhe, Germany
IEEE Intelligent Vehicles Symposium (2020) https://arxiv.org/abs/2002.00497
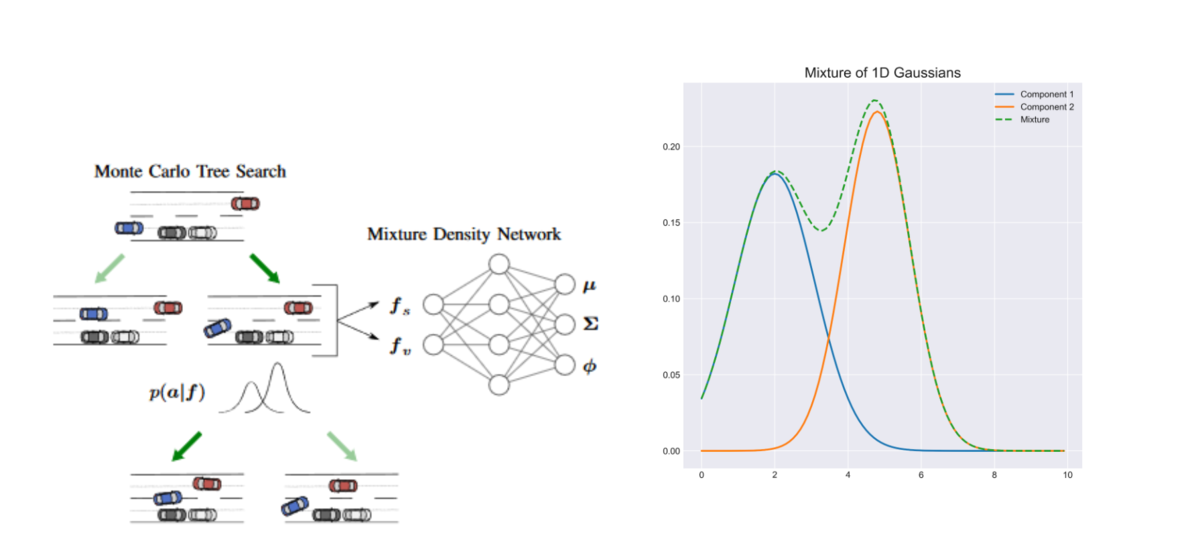
Figure 6 - (a) Use of the Gaussian mixture to select actions in the MCTS (b) Gaussian mixture
(b) taken from https://angusturner.github.io/generative_models/2017/11/03/pytorch-gaussian-mixture-model.html
As discussed in the previous section, MCTS are great to model interactions with other agents but are very hard to sufficiently explore. In order to make exploring the tree more efficient, this paper learns Gaussian mixture models that associate each state (i.e., node of the MCTS) some probabilities on the action space. These probabilities are used to guide the exploration of the tree.
A Gaussian mixture is a combination of several Gaussian probability distributions, allowing multiple peaks with different means and covariances (Figure 6b). In this paper, the actions modeled by these probabilities are pairs of changes in longitudinal velocity and in lateral position. This means that for a given state, the mixture must contain as many peaks as there are possible maneuvers such that their mean will correspond to the typical trajectory for that maneuver. On the highway for example, mixtures with 2 components can be used to learn the 2 typical maneuvers of keeping or changing lanes (Figure 6a).
This technique is interesting to make the exploration faster but the experiments of the paper do not show any performance improvements once enough exploring time is given. Having to fix the number of components can also be an issue when trying to generalize to various situations.
Conclusion
Decision making for autonomous driving remains a very important topic of research with many exciting directions currently being investigated.
Researchers and engineers at Tier IV are working to bring the results of this progress to Autoware as well as to develop new techniques to help make autonomous driving safer and smarter.
