こんにちは、ティアフォーでパートタイムエンジニアをしている吉本です。
本記事では、計算量を抑えつつシミュレータ内のNPCロジックをよりリアルにする手法について紹介します。
なお、ティアフォーでは「自動運転の民主化」をともに実現していく、学生パートタイムエンジニアを常時募集しています。 自動運転という活発に研究開発が行われている分野で生き残っていくためには、自社で技術開発を行っていくと同時に常に最新の論文からキャッチアップし続ける必要があり、論文の内容の実装や改良を行っていくなど、幅広い領域でパートタイムエンジニアの募集があります。
まずは「話を聞いてみたい」でも結構ですので、もしご興味があれば以下のページからコンタクトいただければと思います。
NPCロジック改良の背景
シミュレーションチームでは、こちらの記事で紹介があったようにシナリオテストによって自動運転の安全性担保に取り組んでいます。 様々な交通状況のシーンをシナリオに書き起こしてテストを行うわけですが、現在は人間のシナリオライターが行っています。
シナリオでは道路上の車両はもちろんのこと、自転車や歩行者などのNPC(Non Player Character)までもその挙動を細かく指定する必要があります。 この大きな手間を削減するためにシミュレーションチームではBehavior Treeを用いたNPCロジックの強化を行いました。
この改良により、NPCに関してシナリオを細かく指定しなくてもある程度動くようになり、シナリオ書き起こしの作業負荷は大幅に軽減しました。
ただし、これでも短時間に状態間を行ったり来たりするチャタリング問題が起こったり、ある種類のNPCに対して適用した状態機械を他のNPCに流用しようとすると、状態遷移条件が状態の中に記述されているため簡単には流用できない等の問題が残っていて、現行のNPCロジックでは今後多数のシナリオを書いていく際に大きな懸念事項となります。 また、10体以上のNPCが出現するシナリオもあるため、NPCロジックには計算量の少なさが強く求められます。
NPCロジック改良のインパクト
以上のような問題点を解決するために、私たちはORCA(Optimal Reciprocal Collision Avoidanceの略称)というアルゴリズムを導入することにしました。
今まではシナリオ上で「この速度でこの経路の上を通って動きなさい」といった詳細な”NPCの挙動”を指定していたところを、ORCAでは「この中で動きなさい」というよう動作時に求められる”NPCの挙動の制約条件”を指定するようになっていて、難しい状況に対しても状態のチャタリング現象などが発生することなく動作計画が作れます。
チャタリング現象と言うと難しく聞こえるかもしれませんが、みなさんも歩道などで向こうからやってくる歩行者が右に避けるか左に避けるか分からずに右往左往したことはないでしょうか?
はじめは右に避けることが最適に思えても対向者が同じ方向に避けると最適な避ける方向が左に変わってしまいます。
それを見た対向者が今度は逆の方向に避けようとするともう大変。
同じことが無限ループしてしまい、対面でお互い進路を譲りたいはずなのに妨害して立ち往生してしまいます。
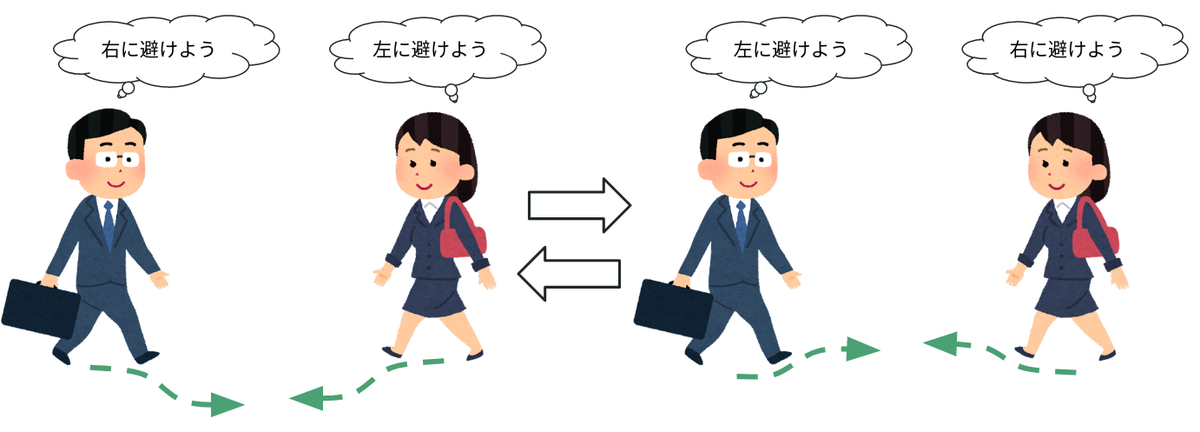
ORCAではそのようなチャタリング現象にもしっかりと対策されているので、導入によりNPCの立ち往生の防止が期待できます。
また、ORCAにおける各NPCの行動計画は独立して計算できるので、並列計算などで計算機のリソースを最大限に活用できます。 また、計算量が少なくなるように設計されていて多数のNPCが出現するようなシナリオでもスムーズに動作します。
ORCAとは?
ORCAは2010年に提案された衝突回避アルゴリズムです。[1] 提案後も様々な改良がなされ、非ホロノミック拘束をもつエージェントに対応したモデル[2]や、市街地環境で複数のドローンを使って環境を効率よくスキャンするといったマルチロボットでタスクを効率よく実行するための制約条件を入れたモデル[3]等も提案されており、様々な応用先が考えられています。 お互いに意思を持つ多数のエージェント同士が衝突を回避するための行動計画をそれぞれ短い時間で計算できます。 10年経った現在では様々な派生手法が発表されていますが、ベースモデルとしてまだまだ現役で使われています。
ORCAでは、速度空間内でのエージェント同士がぶつからないような線形不等式制約を相対速度と距離から作り出し、制約内で最適な(目標速度に最も近い)速度を計算します。 ORCAのスゴイところは、この計算した線形不等式制約がエージェント同士で通信せずともお互い回避できるような制約になっている点です。 普通なら片方が右に避けるからもう片方は左に避けるといったコミュニケーションをとったり中央集権的なアルゴリズムを用いたくなるものですが、ORCAでは各エージェントごとの行動計画は独立して計算できるため、多数のエージェントが存在する場合でも計算を並列化して高速に計算できます。
この制約条件を近くに存在する他のエージェントに対して計算して(下図)、残った速度空間内で所望の速度に最も近い速度をNPCに適用します。
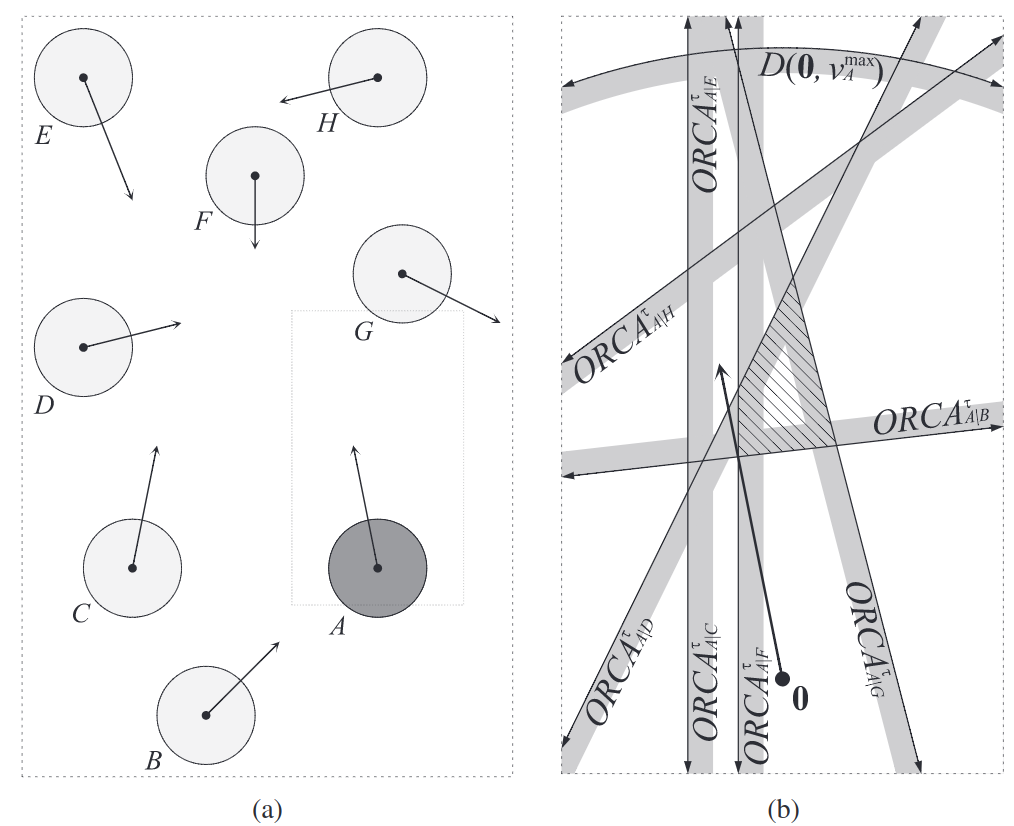
複雑な制約でも線形不等式制約という簡単な制約に落とし込むことで計算が軽くなるように工夫されています。
また、この手法は拡張性の高さも魅力の1つです。 速度空間内の線形不等式制約にさえ落とし込めばその他の制約も追加できるため、例えば自動車なら対向車線に行かないような制約、歩行者なら歩道や横断歩道からはみ出ないような制約を追加することもできるでしょう。
NPCロジック改良の実装とデモ
実はOCRAのアルゴリズムはRVO2というOSS(Open Source Software)のライブラリで公開されているので、それをライセンスにしたがって使わせていただいています。 ただし、実際に使うにあたり、NPCの種類や個体ごとにパラメータや避ける障害物を調整できるようにカスタマイズ版を開発しました。 自動車や人などが通行するときには様々な制約のもとで行動しています。 例えば、道路から飛び出さないといった単純なものから信号が赤であれば停止線より前には行かないといった様々な制約があります。 そのため、このORCAモデル単体では賢いNPCを作ることはできず、そこに交通状況のコンテキストを考慮できる機能を導入する必要があります。
そこで現在ティアフォーのシミュレーションチームでは、scenario_simulator_v2のNPCロジックをプラグイン化し、こちらの論文[4]で採用されているContext-GAMMAというORCAに周囲の交通状況のコンテキストを考慮させたモデルにさらにティアフォー独自のアレンジを加えたNPCロジックを実装中です。
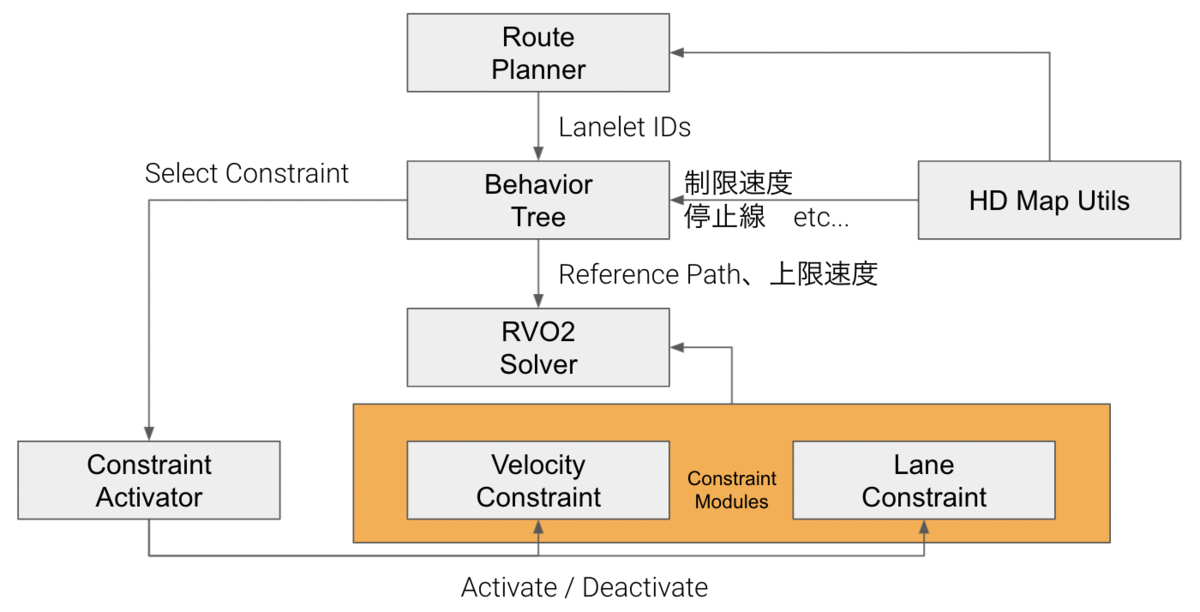
具体的には、Context-GAMMA単体では参照経路は事前に与える必要があるので、参照経路をBehavior Treeアルゴリズムを使用して作成、それにおおよそしたがいつつ衝突等は避けるといった感じの挙動をContext-GAMMAを使用して生成します。 まずは歩行者から実装を開始し、次は自動車、自転車、バイクとどんどん対象を広げられればと考えています。
今後もティアフォーのシミュレーションチームではさらなるシミュレータの高度化およびAutowareの評価手法の自動化、効率化を目指します。
参考文献
[1] Van Den Berg, Jur, et al. "Optimal reciprocal collision avoidance for multi-agent navigation." 2010 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2010.
[2] Alonso-Mora, Javier, et al. "Optimal reciprocal collision avoidance for multiple non-holonomic robots." Distributed autonomous robotic systems. Springer, Berlin, Heidelberg, 2013. 203-216.
[3] Arul, Senthil Hariharan, et al. "LSwarm: Efficient collision avoidance for large swarms with coverage constraints in complex urban scenes." IEEE Robotics and Automation Letters 4.4 2019. 3940-3947.
[4] Cai, Panpan, et al. "Summit: A simulator for urban driving in massive mixed traffic." 2020 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2020.