Motion Planning Under Various Constraints - Autonomous Parking Case

Introduction to the Motion Planning

Autonomous vehicles (robots, agents) are requested to move around in an environment, executing complex, safe maneuvers without human interference and to make thousands of decisions in a split second. How can we endow autonomous vehicles with these properties?  

By the way, at Tier Ⅳ, we are looking for various engineers and researchers to ensure the safety and security of autonomous driving and to realise sharing technology for safe intelligent vehicles. Anyone who is interested in joining us, please contact us from the web page below. 

tier4.jp

Then, the key to answering this question is “Motion Planning”. Autonomous vehicles should be able to quickly generate motion plans and choose the best among many or the optimal plan defined by some optimization criteria. 

Motion planning modules for autonomous driving might serve for three different objectives [1]:

• Producing a trajectory to track,
• Producing a path to follow,
• Producing a path and trajectory with a definite final configuration. 

In a trajectory tracking task, agents execute time-stamped commands to satisfy the spatial coordinates with the prescribed velocities. In the path tracking, only positions are tracked. 

Vehicle motion is formally defined using a couple of differential equations. These differential equations propagate the state variables such as velocities (Longitudinal and lateral velocities; Vx, Vy and Heading Rate ) in the chosen coordinate system. The resultant integral curves define the configuration space of the robots (see Figure 1.). If we are controlling robots by velocities, the motion equations are called kinematic model equations.

Figure 1. Configuration space (x, y and heading rate) for a car-like robot motion

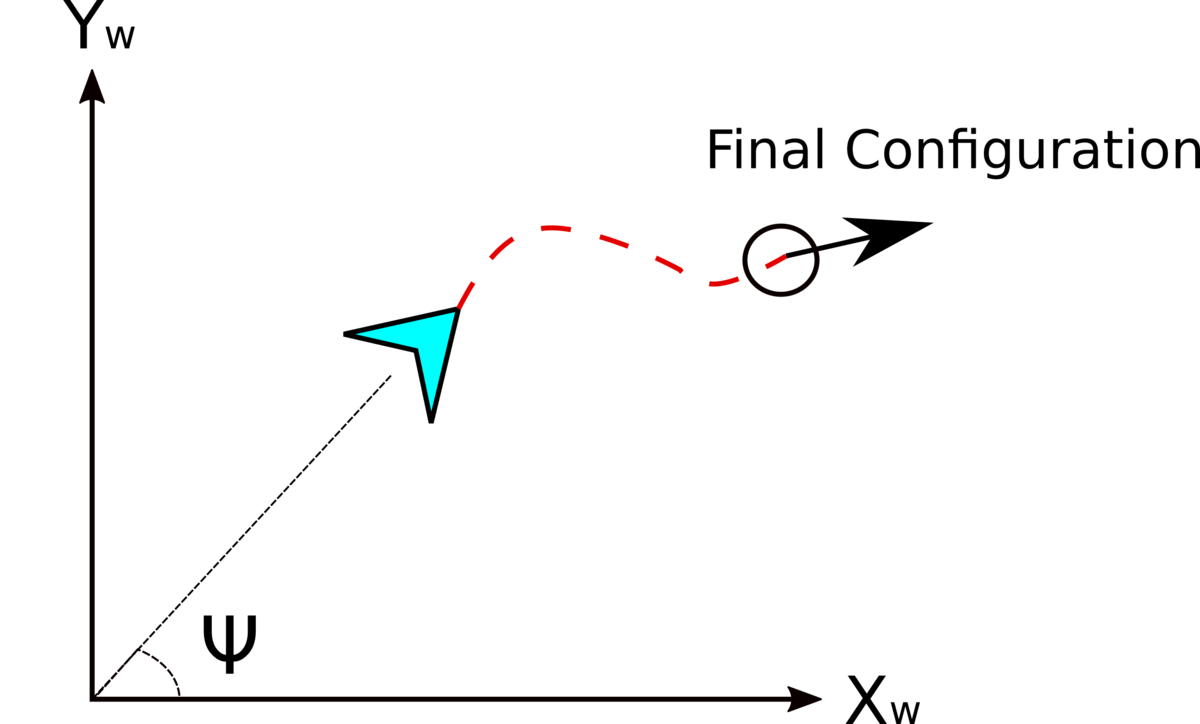
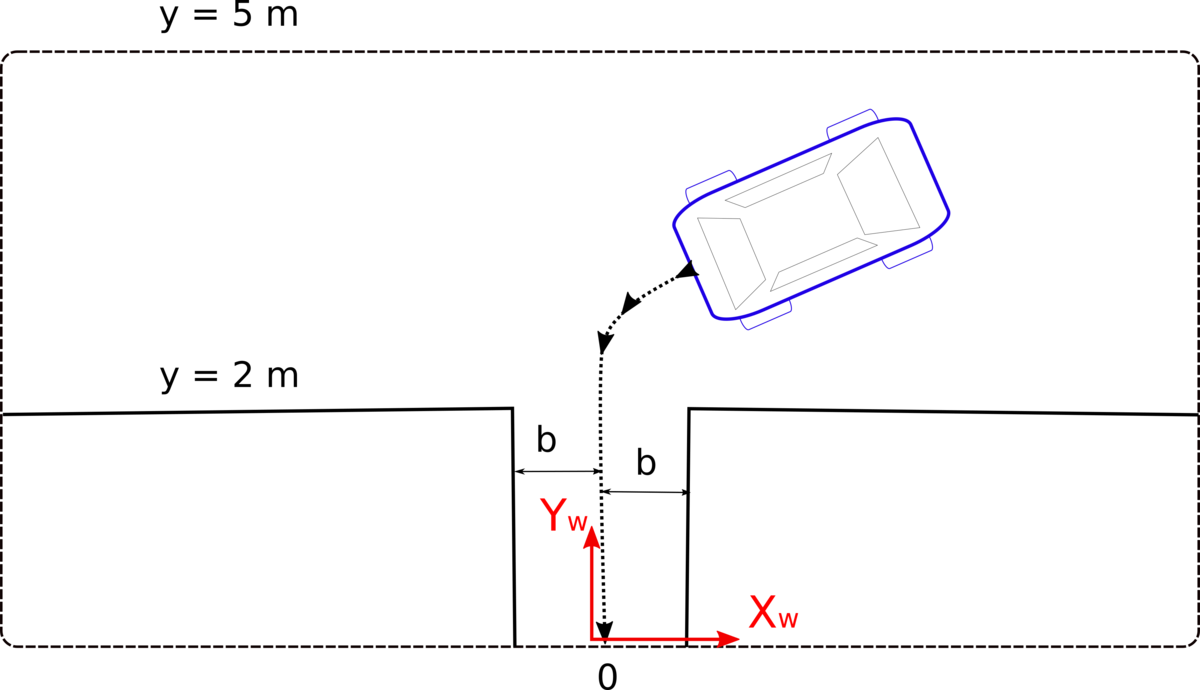
The most difficult task in the objectives list is the last one: to generate a trajectory or a path while satisfying the endpoint configuration. We are familiar with this kind of planning tasks from our daily life. You can probably remember how frustrating it was to park a vehicle within a parking slot the first time and execute a couple of maneuvers without hitting the cars or walls around (Figure 2).

Figure 2. Parallel parking

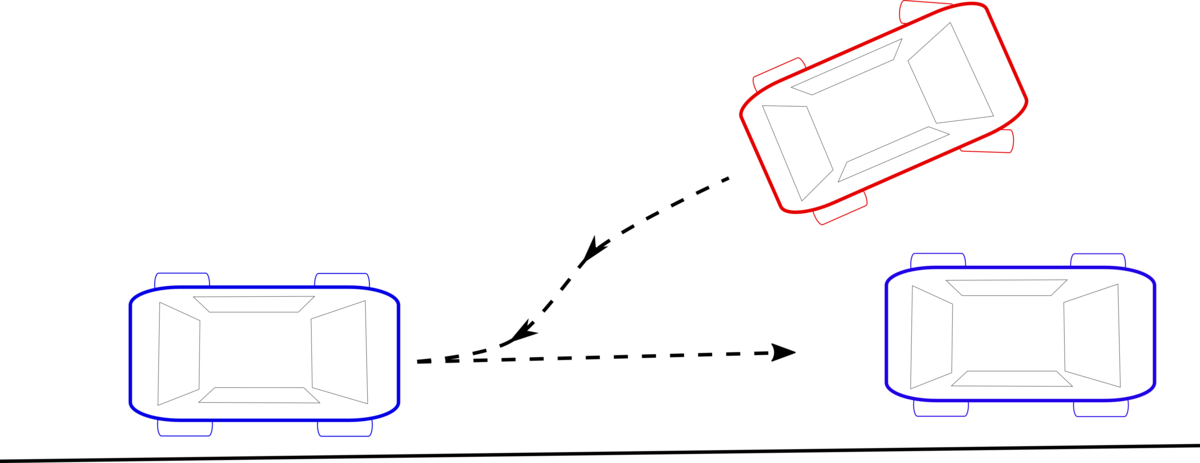
 Why is planning with the endpoint configuration a difficult task even for cases without any obstacle in the environment?

When considering the parking maneuver, notice that a car can only move forward-backward directions. If we also turn the steering wheel, the vehicle follows a circular path. Cars cannot move in their sideway direction as it is impossible due to the fixed rear wheel orientation. On the other hand, while executing a parking maneuver, we need to be able to move the car in the sideway directions to properly park the vehicle. That is why we drive the car, backward-forward and steer to move the car’s position in parallel to the starting position (Figure 3).

Figure 3. To move the car in the sideway direction parallel to the starting configuration, we need at least two maneuvers.

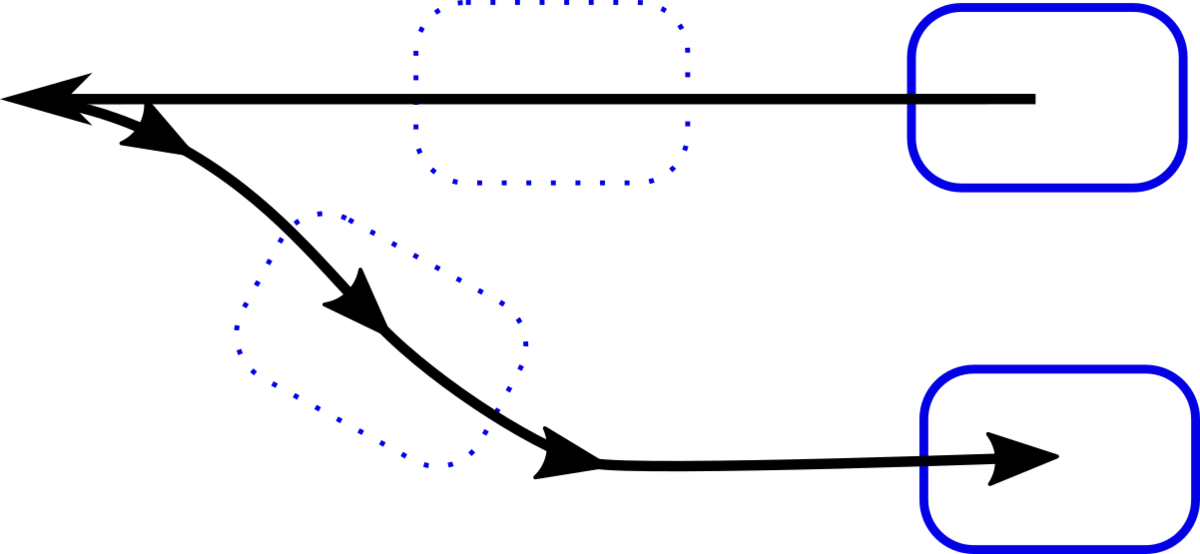
In physics, the prohibited sideway directions mean zero velocity in these directions. Although there are no environmental obstacles or physical constraints in these directions, the velocity is constrained to be zero. We can not integrate these velocities to convert them to path constraints which are relatively simpler to deal with. These velocity constraints are called "non-holonomic" motion constraints.

Since we have three motion direction (x, y and heading angle) and two controls (Speed V and steering δ), these kinds of systems are called under-actuated. Non-holonomic systems are in general under-actuated. Finding a path given two configuration positions respecting the velocity constraint is difficult due to the missing control direction.

Almost five decades of research effort has been put into finding a solution for non-holonomic motion planning. There has been no general solution proposed so far to the problem. Although it is possible to move a car position in parallel with a couple of maneuvers, such as zigzagging (Figure 3), the resultant paths and trajectories are discontinuous and generally have some cusp and breakpoints.  This makes the solutions more difficult to find smooth trajectories mathematically. The nonholonomic motion planning problem becomes even more difficult when there are constraints in the environment (such as parking a vehicle in between the other vehicles).  What is more, the motion equations are usually nonlinear and nonlinear differential equations do not have a direct solution except in a few cases.

In the robotics literature, approximate solutions have been proposed. These solutions are based on the notion of local controllability and the geometry of the configuration space. In principle, a global motion between two endpoints is divided into small motion trajectories. The small motion intervals are then connected using various algorithms.

When there are no obstacles in the environment, we can use Reed & Shepp Curves (R&S Curves) to generate a direct path given two endpoints [2]. The R&S curves fit a path for the given endpoint configurations using some motion primitives; Straight (Backward-Forward), Left - Right Turns (Forward-Backward). 

A couple of examples of R&S curves are shown in the following figures [3]. 

Figure 4. Reeds and Shepp curves for two different endpoint conditions.

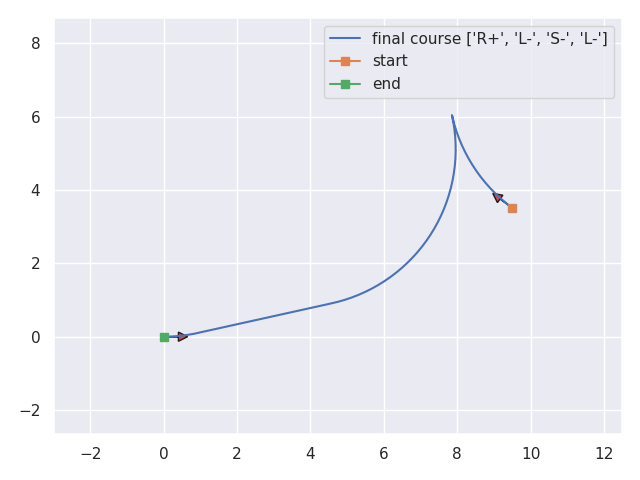
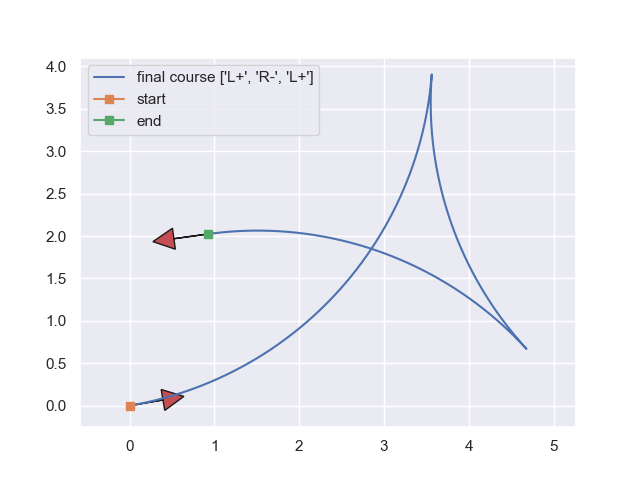
Even though the R&S curves produce time-optimal and pleasing curves, they cannot provide a solution when there are environmental constraints. Their use is limited to unconstrained cases. 

The most recent literature focuses on two-staged nonlinear optimization-based solutions for constrained environments.   Nonlinear Optimization (Nonlinear Programming techniques - NLP) can deal with nonlinear motion equations and constraints. However, the nonlinear optimization methods require a good feasible solution to start with. This difficulty is what diversifies the proposals in the literature. We can list these methods under four categories. These are;

• Optimization-based (bi-level or multi-staged optimization)
• Heuristic algorithms (particle swarm optimization, genetic algorithm)
• Sampling-based algorithms (RRT, Hybrid-A*) and, 
• Machine learning. 

The proposed algorithms have advantages and disadvantages relative to each other. The common theme of these algorithms is having a two-stage solution that contributes to the implementation complexity.

At Tier IV, we have proposed a new algorithm for autonomous vehicle parking maneuvers inspired by an optimization method trending in the aerospace industry for designing spacecraft trajectories. The Successive Convexification Algorithm (SCvx) is capable of returning a feasible trajectory under a wide range of initial conditions, removing the need for a two stage approach, and has been proven to converge to the solution of the original nonlinear problem without compromising accuracy. In the next section, we explain what kind of problems we can encounter in the numerical solution of optimization problems, and how the successive convexification methods offer a solution to constrained nonholonomic motion planning.

Solving Nonlinear Problems by Successive Convexification Algorithms

Apart from a very demanding feasible initial solution in nonlinear programs, a design engineer can experience infeasible solution error messages raised by the solvers used in the numerical problem although the original problem is feasible. This kind of infeasibility is called artificial infeasibility. Solvers in numerical optimization have a mechanism to check beforehand whether the problem is feasible or not. The cause of infeasibility can be attributed to the results of implicit or explicit unrealistic linearization. 

Furthermore, linear functions might not have a lower bound in the search space. This could be another reason for the solvers to halt. The lack of a lower bound in a minimization problem is called “artificial unboundedness” [see 3, 4, 5 and references therein]. 

The SCvx algorithm is a kind of sequential quadratic optimization. In the sequential solutions, the nonlinear motion and constraint equations are linearized starting from an initial trajectory. Almost in all mathematical problems, one of the best strategies for the solution is to convert complex problems into a series of linear problems.

The solution of a linear problem yields a feasible trajectory which is then used as an initial trajectory for the next solution (Figure 5).

Figure 5. A nonlinear trajectory can be approximated by linear sub-problems which can be solved iteratively.

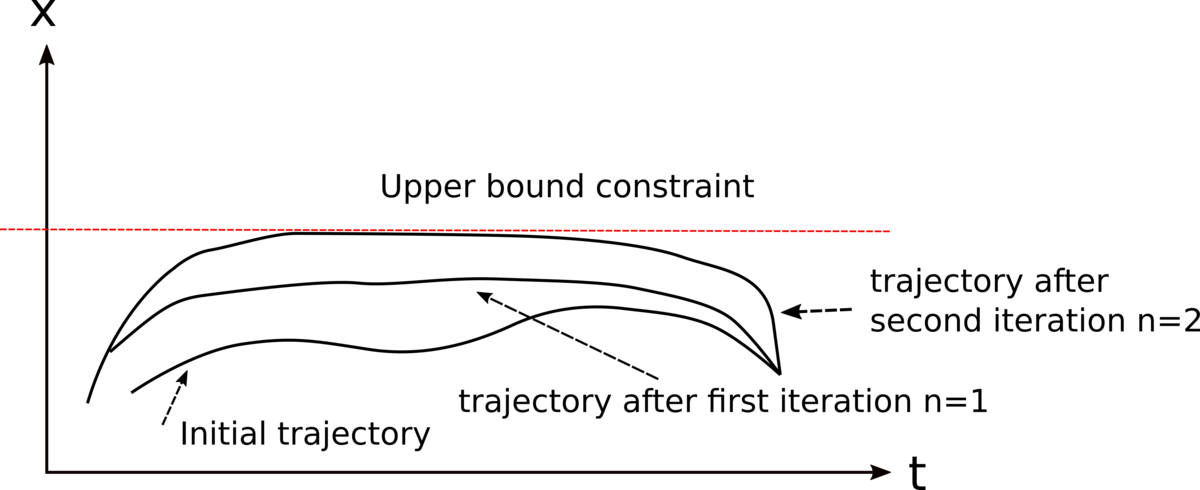
The SCvx algorithm operates in the same manner with two additional mechanisms to prevent artificial infeasibility and artificial unboundedness error messages. 

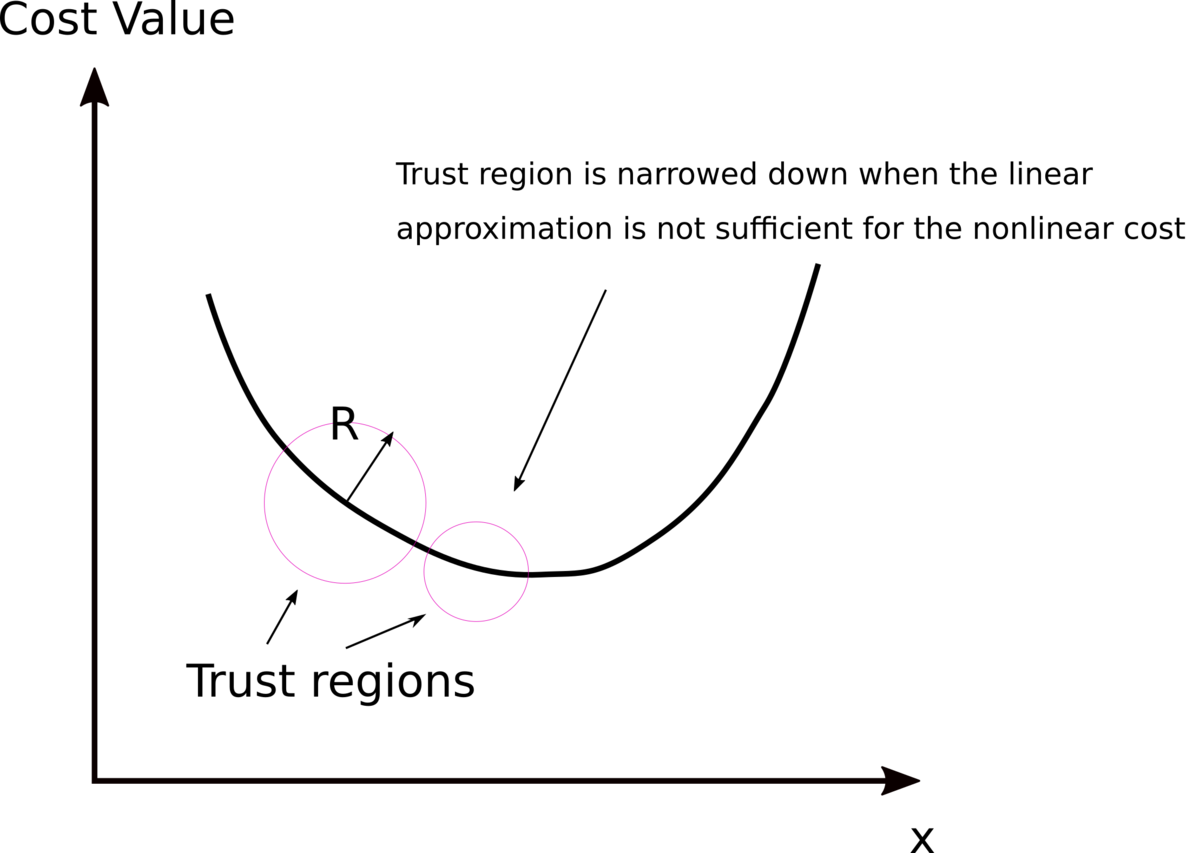
The artificial unboundedness problem is addressed by introducing a trust region that restricts the search space (Figure 6). The radius of the thrust region is adjusted by checking if our linearization reasonably approximates the nonlinear cost. If the linearization approximates the nonlinearity well enough, the radius of the trust region is increased, and vice versa.

Figure 6. Trust regions are used to restrict the search space of the optimization algorithm. The minimum or maximum is sought within the circles specified by the trust region radius.

The artificial infeasibility problem is addressed by adding a virtual force pushing all the infeasible states into a feasible region. However, the amount of virtual force we apply is penalized in the cost function with a very high weighting factor (i.e 1e5). One of the objectives is to make the contribution of the virtual force to the cost zero in the optimization. 

These two additional mechanisms to prevent artificial infeasibility and unboundedness prevent the solvers from stopping due to the numerical problems and allow the solvers to seek the solution. The SCvx algorithms have been proved to converge to the original nonlinear solution. When a solution of the linear counterpart of a nonlinear problem is equivalent, the solution is called lossless (no feasible region is removed from the problem, [5]).

How Does the Successive Convexification Algorithm (SCvx) Help in Solving the Autonomous Parking (Nonholonomic Motion Planning) Problem?

So far, we alluded that the SCvx algorithm could give us a solution for a nonlinear optimization problem by solving sequential linear sub-problems. We also emphasised a virtual force that pushes infeasible states into the feasible state-space regions, and later on, this force is driven to zero. These two properties eliminate the need for a feasible initial trajectory, therefore reducing the two-stage solutions into one. The SCvx algorithm does not require an initial feasible trajectory. This is a highly desirable property since it is generally a hard problem to come with an initial trajectory in nonlinear optimization problems.  

Although we are now closer to the solution for an autonomous parking problem, we need to overcome the other continuity issues afflicted.  When we have a look at the R&S curves, point-to-point trajectories might require forward-backward - full stop motion. The vehicle moves a bit forward, stops fully, makes a full steering turn and moves back. There are both input and output discontinuities. The solvers and optimization algorithms operate on the continuity assumption. The second issue is the discontinuities in the environmental constraints. 

Inspired by the shape of R&S curves, we divide a whole parking maneuver into a minimum of three curve sections. Most of the trajectories that the R&S method produces consists of a maximum of four or five connected curves. Dividing a whole trajectory into three sections captures most of the solution families. In this proposal, we can imagine three separate vehicles trying to reach each other similar to the situation we see in a flag race (Figure 7).

Figure 7. Three separate curve sections on which each vehicle travels.

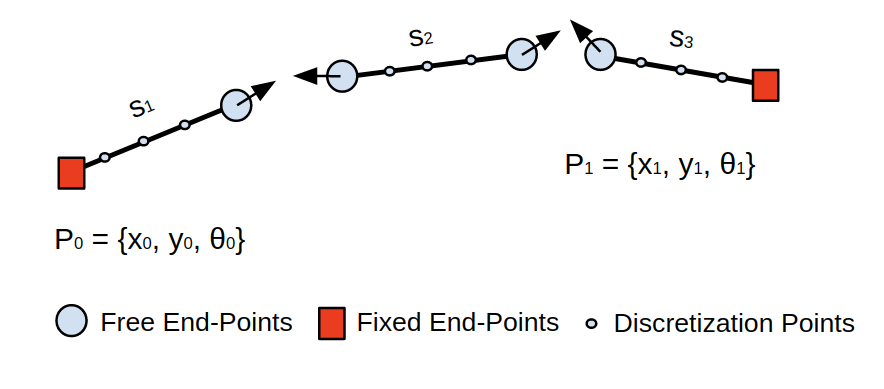
The three separate-curve-approach  can be formulated with boundary conditions for each curve. The start and endpoint of the whole trajectory must be fixed. The curve connections (light blue circles) are the free boundary conditions for each of the curves that are needed to be connected by the optimization algorithm. In this way, we can obtain any arbitrary trajectory with cusps and breakpoints 

A solution to a nonholonomic motion planning problem without environmental constraints using the SCvx algorithm is shown in Figure 8.

Figure 8. A trajectory with two cusps solved by SCvx for an unconstrained case. The arrows with red-hats show the direction of the vehicle.

For the second issue; discontinuities in the environmental constraints, we used a state-triggered constraint formulation offered by the same authors of SCvx algorithms [5]. The authors formulate the keep-out zone for the spacecraft landing regions using the state-triggered constraints. The keep-out zone formulation resembles parking situations. In some optimization problems, we need to define the regions where  some constraints could be active or inactive. This requires logical constraints or binary decisions such that, if some conditions occur, then some constraints are activated [if the triggering “condition < 0” ⇒ constraints < 0]. In mathematical optimization theory, these kinds of logical constraints are solved by mixed integer programming which is equally as hard as nonlinear optimization. We show an example of triggering and constraint conditions in Figure 9.

Figure 9. State-triggered constraint condition for a parking lot. Here the triggering conditions are xw < - b OR xw > b. When these conditions are triggered, the vehicle’s position value in yw direction must be yw>2 meters.

As you may notice, the solutions obtained at each iteration becomes an initial trajectory for the subsequent problem and hints us the regions where the logical constraints become active or inactive.  This allows us to inject discontinuous environmental constraints when the iterated trajectory triggers the condition. 

Using the state-triggers eliminates the use of complicated collision checking algorithms and alleviates the load of the solvers.

Complete Solution for Parking Maneuvers

We applied the strategies we have mentioned to a couple of tight parking scenarios: parallel and perpendicular parking, which are shown in figures 10 and 11 respectively and with an animation in Figure 12. In these figures, we compare the SCvx solutions to the R&S curve solutions that are not aware of any constraints in the environment.

Figure 10. A parallel parking case. The vehicle starts in a random position and direction in the green shaded area and is requested to park in between two obstacles parallel to the X-axis.

Figure 11. A reverse parking case. The vehicle is requested to park perpendicular to the X-axis in between two obstacles.

Figure 12. An animation for a reverse parking maneuver.

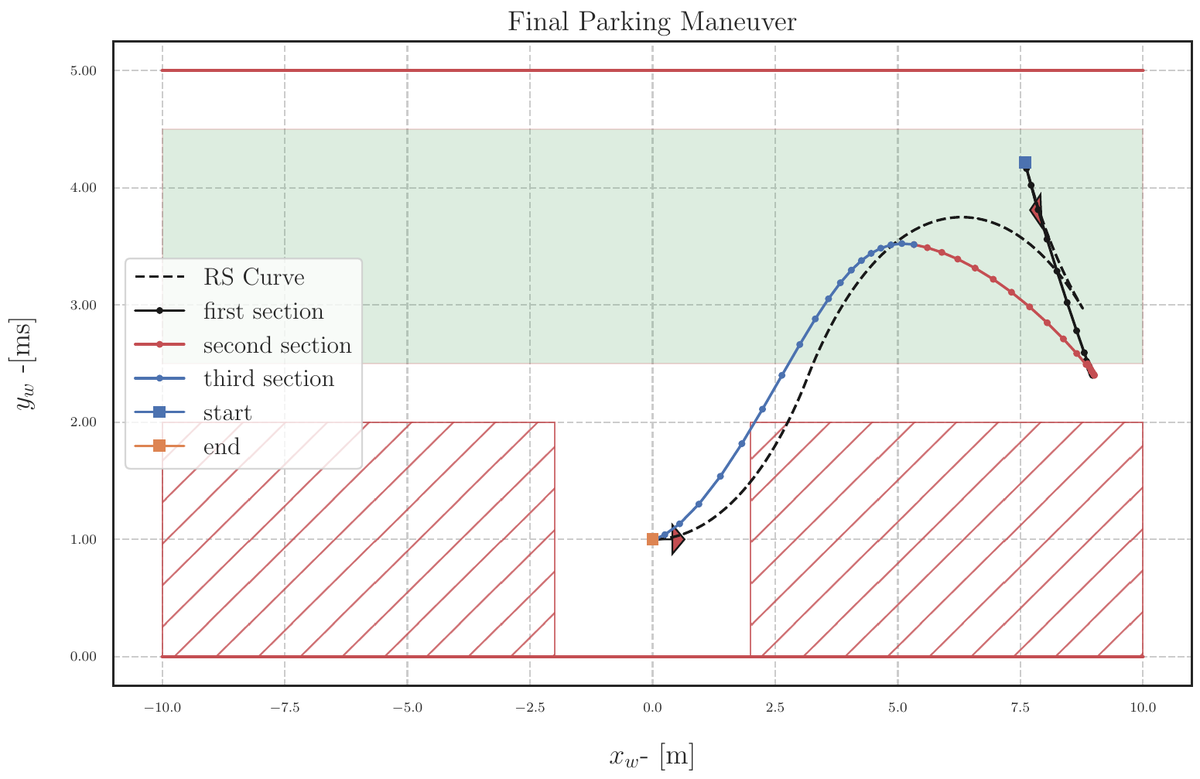
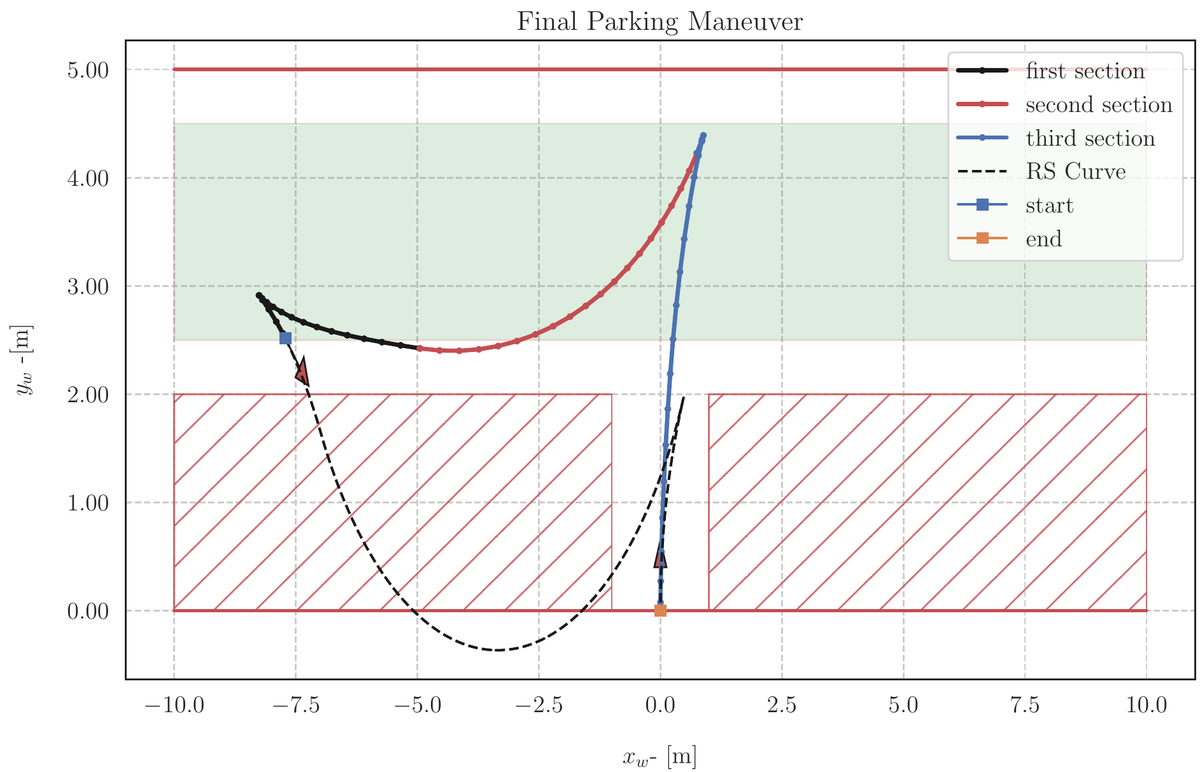
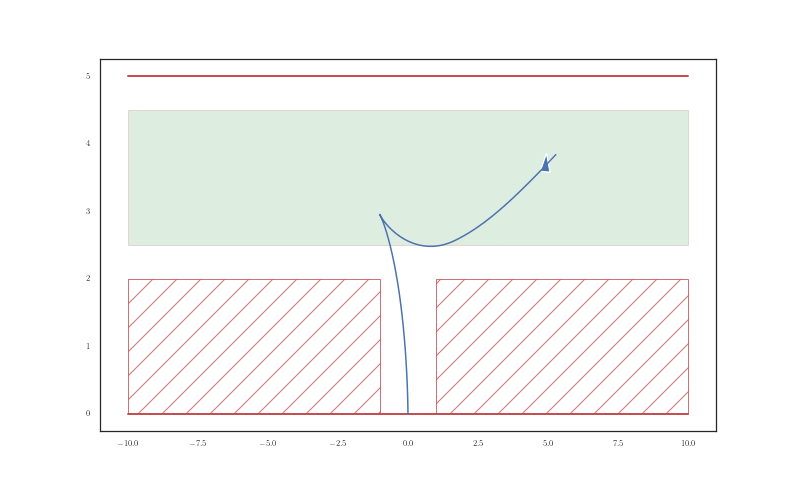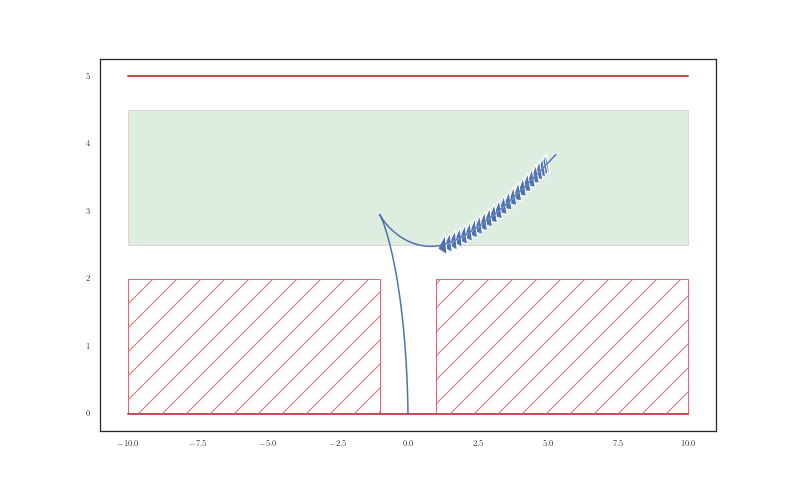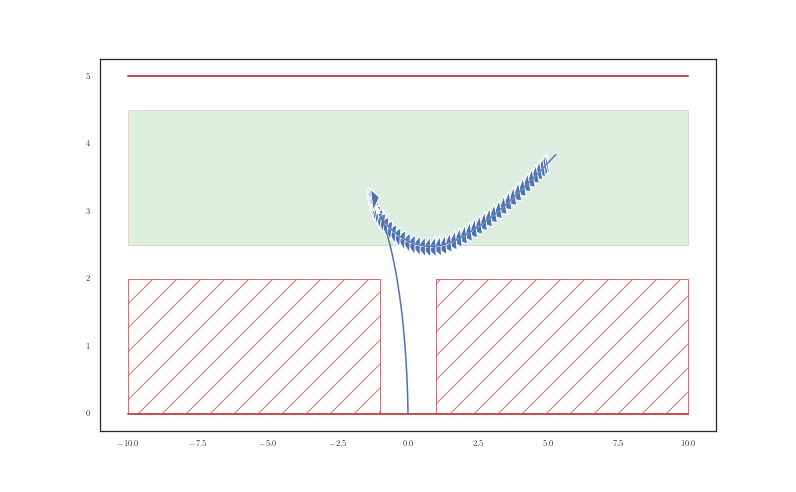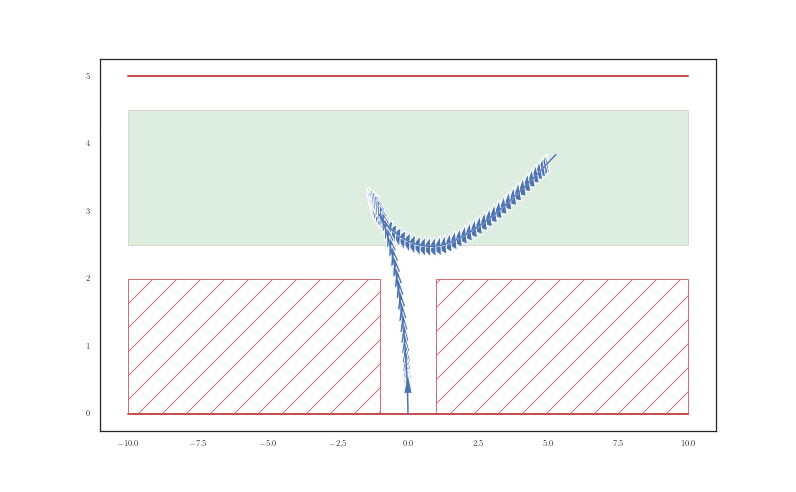
Final Remarks

In this blog article, we summarized one of our publications presented at ITSC 2020; “Autonomous Parking by Successive Convexification and Compound State Triggers”. The detailed algorithms, equations and procedures and the related literature review and references can be found in our paper. We are planning to put the application of SCvx solutions into Autoware.

References:

1. Latombe, J.C., 2012. Robot motion planning (Vol. 124). Springer Science & Business Media.
2. LaValle, S.M., 2006. Planning algorithms. Cambridge university press.
3. Boyali, A. and Thompson, S., 2020, September. Autonomous Parking by Successive Convexification and Compound State Triggers. In 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC) (pp. 1-8). IEEE.
4. Mao, Y., Szmuk, M. and Açıkmeşe, B., 2016, December. Successive convexification of non-convex optimal control problems and its convergence properties. In 2016 IEEE 55th Conference on Decision and Control (CDC) (pp. 3636-3641). IEEE.
5. Szmuk, M., 2019. Successive Convexification & High-Performance Feedback Control for Agile Flight (Doctoral dissertation).

http://larsblackmore.com/losslessconvexification.htm